高斯过程回归(Gaussian Process Regression)是一种结合先验进行回归分析的非参数概率模型。利用高斯过程可以优雅的实现小样本回归,并且能够让人直观的感受回归效果,尤其是其优美的分布特性引人入胜,在笔者看来,是一个不错的预测回归工具。
高斯过程在近几年也有不错的发展,关注到 Raissi (2017) 提出一种利用GPR绕过求解微分方程步骤,直接学习的方程中的系数的方法,可适用于例如扩散场求解等各种工程问题。本文将概述高斯过程核心理论,同时尝试代码实现利用高斯过程学习抛物线型微分方程的系数。
en 标题起的不太准,懒得改辽
1 高斯过程简介
本部分将谈到多维高斯分布,边缘分布与条件分布,以及高斯过程的个人理解。从熟悉的一维高斯分布容易扩展到二维以及多维的高斯分布,推导及相关性质不再赘述,可参考:
1.1 多维高斯分布
无论是一维高斯分布还是多维高斯分布,其分布特性都由均值向量和协方差矩阵确定。假设向量 𝑋 服从均值为向量 𝜇,协方差矩阵为 𝐾 的高斯分布,本文记为:
上式中向量 𝑋 由随机变量组成(每一个随机变量都服从正态分布,因而随机变量的联合分布也是属于高斯分布的),均值向量 𝜇 描述的是向量 𝑋 的分布的期望,而协方差矩阵 𝐾 用以记录描述每个随机变量之间的关联,是一个对称的半正定矩阵:
1.2 高斯分布的边缘与条件分布
由于高斯过程回归会应用到贝叶斯公式计算后验概率,因此需要考虑随机变量的条件分布与边缘分布的计算。推导过程可参考:
不出意外,高斯分布的条件分布与边缘分布仍然是高斯分布,这是最最最吸引笔者的地方,此外也贝叶斯推断变得容易求解。
若假设随机变量 X, Y 的联合分布服从高斯分布:
那么条件概率的计算公式为:
此时将联合概率分布对要边缘化的随机变量进行积分,可以计算出边缘概率分布:
由上式计算可得:
1.3 高斯过程概述
高斯过程可以看作是高斯分布从离散域到连续域的扩展,是一种由有限维度到无限维度的延伸。随着维度的升高,可以看作随机变量 X 由是由函数𝑓(𝑥) 采样得到的,那么原来的高斯分布就变为:
若对于定义域内的所有的 𝑥∈𝐷 上式都成立则称 𝑓 是一个高斯过程,表示为:
上式中,𝜇(𝑥) 表示均值函数(Mean Function),𝑘(𝑥,𝑥) 为协方差函数(Covariance Function),常用核函数表示,本质上是描述随机变量之间相互影响的函数。
2 基于GPR的Raissi方法实现
直接的高斯过程回归十分优雅,按照笔者的理解,这是一个利用采样信息去计算贝叶斯后验概率的过程。而关于普通的高斯过程回归(或者分类)的实现,无论是自己敲点代码还是利用如matlab工具箱、SKlearn等现成工具包,都能较为方便完成。直接的高斯过程回归的理解与实现可参考:
值得注意的是,直接的高斯过程回归可以进行核函数优化以得到更好的概率分布。而 Raissi 在 2017年提出利用参数优化过程结合高斯过程的分布特点,实现抛物线型微分方程参数的传递与求解的方法。下文将尝试实现这一方法。
2.1 核函数
常见的基本核函数(kernel function)有径向基函数核、周期核、线性核、常数核等。这些核函数都有各自的特性,比如径向基函数核为平稳核,协方差矩阵只取决于随机变量的相对位置;周期核函数顾名思义具有周期性,协方差矩阵沿对角线将会出现规律性分布。本章采取的核函数为径向基函数核:
上式中, $\theta=\left(\sigma, w_{d}^{i}\right)$ 为核函数的超参数(hyper parameter),$w_{d}$ 为自动相关确定权重(Automatic Relevance Determination, 简称ARD)。直观上$w_{i}$ 影响高斯分布的平滑程度,超参数 σ 将影响高斯分布与均值之间的距离.


如图,淡蓝色区间为高斯过程的置信区间,蓝色实现为高斯过程的均值分布。可以看出随着$w_{i}$的增加,高斯过程更加平滑;随着超参数σ的减小,高斯过程分布更加集中。
利用高斯过程在贝叶斯最大化后验概率中学习超参数的值,该方法采用L-BFGS算法求解对数边缘似然的最大值,也就是:
需要说明的是,后验概率随超参数的分布是一个非凸问题,如果优化初值设置不合理,会陷入局部最优,且在没有先验知识的情况下难以对超参数的初值进行估计与调整,目前常用的有效方法还是通过改变初值重复计算来尽量找寻最优解。此时观察可知,核函数 K 的计算是整个问题的核心所在。
2.2 一维扩散方程
由菲克定律,渗透扩散问题的线性偏微分微分方程的形式为:
若假设函数 𝑢 是一个高斯过程:
那么函数 𝑢 经过线性过程得到的函数 𝑓(𝑥,𝑡) 也是一个高斯过程:
核函数 $k_{u u}(x, x)$ 与核函数 $k_{f f}(x, x)$ 之间的关系为:
$k_{f f}(x, x)$描述了函数 𝑓 与函数 𝑓 之间的分布关系,同样的函数 𝑓 与函数 𝑢 的关系,函数 𝑢 与函数 𝑓 的关系可以表示为:
此时考虑函数 𝑓 与函数 𝑢 的联合分布𝑋=[𝑓,𝑢],𝑋服从高斯分布,其协方差矩阵为:
其中,$\sigma_{u}$、$\sigma_{f}$ 为函数 𝑢 与函数 𝑓 的采样噪声估计,不难看出,若 $k_{u u}$采用上述的径向基核函数,那么上式的超参数为:
至此,计算得到了一维扩散问题的核函数K,结合上一节,通过超参数优化过程,可以求解最合理的扩散系数D,完成扩散方程的参数学习。
2.3 处理细节
到目前为止,理论上能够计算抛物线型微分方程中的系数,但是离代码实现与工程应用还有两点细节处理,一个是核函数的代码计算方式在参数传递之后变得尤为复杂,另一个是回归过程的采样数据难以获取(很难测得渗透内部的时刻浓度)。
2.3.1 理论模型修改
用 Fick定律进行分析对原微分方程进行改造以适合工程实际。
带入Fick第二定律中有:
对比可以得到:
此时,原微分方程转化为:
工程实际中,出口的渗透速率容易测量,此时整个扩散问题的处理方法才具备应用价值。
2.3.2 核函数计算
笔者在代码实现过程中,尝试过用计算微分的函数包简化核函数计算,遗憾未实现(看官有好的建议一定一定告诉我!),故而一定程度上简化原核函数并采取暴力计算,公式推导结果如下:
上述式子中,笔者计算的各阶偏导数为:
此时,超参数为:$\theta=\left(D, \sigma, l_{x}, l_{t}, \sigma_{u, f}\right)$
2.4 代码实现结果
笔者迁移 sklearn 中高斯过程的实现模式,模仿其接口风格,完成了适用于RBF核为基本核,线性算子为上文中 $\mathcal{L}_{x}^{D}$ 的高斯过程回归(二维)。代码整理后将发布到 github,或者欢迎邮件联系。
2.4.1 超参数取值空间优化
前文已述,超参数优化是个非凸问题,而核函数计算又比较复杂,初值选取不当很容易导致优化问题无解,所以笔者先用控制变量法手动调节超参数学习初始值,凭借一定经验判断较为合理的超参数优化区间,如下图可观察优化过程:
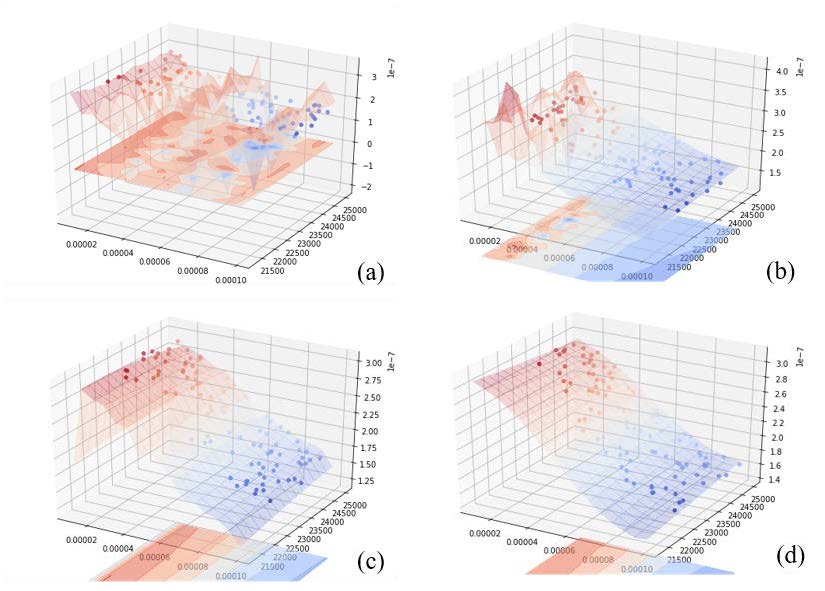
图中(a)到(b)优化了长度尺寸超参数 $𝑙_{𝑥}$ ,由(b)到(c)优化了时间尺寸超参数 $𝑙_{𝑡}$ ,由(c)到(d)优化了增益 𝜎 与噪声评价超参数 $\sigma_{u, f}$。如图可见,随着超参数优化区间的调整,拟合曲面逐渐平坦且合理,虽然依照经验调整无法达到最优区间甚至导致过拟合,但是作为超参数的取值区间,只要后续超参数优化时不碰到区间边界即可减少主观影响。超参数优化过程可继续深入研究。
2.4.2 高斯过程预测
高斯过程回归经过参数优化之后,能够对核函数影响区间内的采样点做出预测,预测原理为通过训练点计算后验概率,若只关注微分方程中的系数其实不用进行预测,但是高斯过程预测能够直观观察回归情况,计算方式为:
式中:$P=\left[k_{u u}\left(x_{p}, x_{u}\right) \quad k_{u f}\left(x_{p}, x_{f}\right)\right]$ , $Y=\left[u\left(x_{u}\right) f\left(x_{f}\right)\right]$
通过差分仿真获取微分方程理论数据进行回归对比,随机采样扩散前期数据(40 points)进行学习,得到的回归预测分布如图:

图中微分方程系数的学习误差为 3.7%,有不错的精度。
3. 总结
直接的高斯过程回归目前已经发展的相对成熟,应用范围广,主要是形式好看十分吸引笔者。此处推荐两本相对容易入门的书(我也只看了一点)
推荐阅读
C.E. Rasmussen. Gaussian processes in machine learning.
K.P. Murphy. Machine learning: a probabilistic perspective.
按照论文,笔者基本实现Raissi方法。由于初值选取有点玄,我调参经验也不是很足,不能达到Raissi(2017)中同样方程的精度,此外有以下不足:
- 计算精度严重依赖初值,并且容易陷入局部最优,奇异矩阵中断求解等情况。Raissi在文中也提到采用合适的数据能得到很好的处理结果。所以我对这种方法的工程实际应用存疑,对论文中极其理想的结果也有一定怀疑。
- 对于不同的方程,核函数的计算要重新构造,需要新的计算方式简化核函数的微分。
- 直接的高斯过程能够实现采样点覆盖范围内的预测,但是在远离采样的地方,难以影响协方差矩阵,笔者认为原理上是不能实现有效预测的,要实现前期样本预测后期数据分布等功能,需要加入如Raissi方法依赖的微分方程等先验知识。
此外,高斯过程计算空间复杂度较高,实现大样本的高斯过程回归有助于提高模型稳定性,可继续研究。